I always tend to jump in others threads. I am pretty well educated. Took a solid 2 years of physics. General and Advanced Physics. Nuclear, or what was called "Modern Physics". Calc 1 and 2, Differential Equations, Engineering Equations, Quantam Math. General Chemistry, Physical Chemistry, Organic Chemistry. Never practiced, was a subcontractor in the light commercial construction industry. My degree is in accounting, again, never practiced, 1 semester from a Masters Degree.
I never liked computers. In the 70's, my high school had one, no monitor. With a paper and pencil I could compute the problem faster, than the computer. It had to send my program somewhere, then a week or two later, a very large piece of green and white paper with a little sentance somewhere in the middle, had my answer. A computer to me has always been just a tool, the most used tool on my computer is the calculator, usually 2 or 3 calculators are open when this computer is turned on. The second most used tool is Cad. Then QuikBooks. I can build a computer, nowadays, for my needs, I get someone I know to build one for me, usually about $300 for parts, $100 labor.
Engineering Equations, we made a lot of graphs. I took a lot of advanced Economics, made a lot of graphs. I can interpret this following chart. Can't use it. It gives me the information I need to backward engineer, to get the information I need. These charts are in fact useless. But, I am a going to use it.
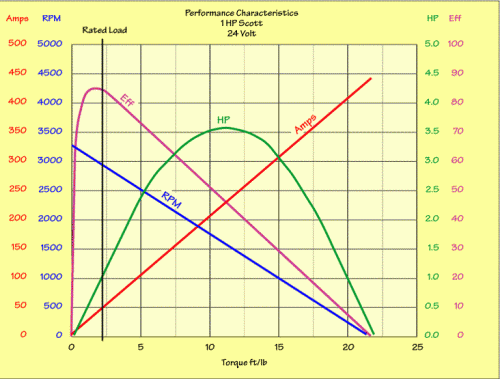
The Scott Motor is rated for 3000 rpm. At 25 mph, my Scott is spinning at 3200 RPM using 10.4 to 1 gear reduction and a 27 and 1/4 tire diameter.
Now the Physics Starts. The Motor is rated at 41 amps. My batteries supply 25 volts. That's 1025 watts. At 3200 rpm, listen, I round off, no reason not too, there is'nt any hard data, I'm only 65% efficient, according to the chart, remember i before e except after c,. .65 * 1025 watts is about 750 watts, or, a 1 hp motor.
So it takes about a HP to go 25 mph on the flat.
But, if I use this chart and re-gear so that the motor is spinning at 2800 rpm, the effiency is 83%. Well this is simple, (83-65)/65 is equal to about a 25% increase in efficiency if I gear taller to reduce my motor rpms.
wheel=27.25x3.14= 85.5" 85.5"/12=7.13' 5280'/mile revolutions/mile=5280/7.13= to about 740 rev/mile.
25miles/hour * 5280ft/mile * rev/7.13ft * 1 hour/60min = the tire traveling or spinning at 308 rpm. 308 * 10.4 = motor rpm of about 3200rpm. To calculate my new reduction ratio, I need a wheel rpm of 308 rpm, I need a motor speed of 2800 rpm for max efficiency, 2800/308= 9.1 ,, I need a 9.1 reduction for a better effiency.
My gut instinct, overall, I will loose efficiency by doing this, too many stops, too many hills. But, I'm a gonna do it, why, motor is too hot, that 35% inefficiency is going to heat. Heating my motor.
Right now, I don't have an amp meter hooked up. but, basically, I have a voltage drop of 1.2 volts on 24 volt system to go 25 mph. Accelerating and going up hills, I have a voltage drop of 2 volts. Range is 14 miles to 10% battery capacity, hard driving, lots of stops and lots of medium hills. This information gives me a lot more data than that useless gragh. Emperical proof.
I am going fishing, see you next week,
chuck




Deafscooter is Here...

=
=
=
Craig installed 1 HP Scott Motor on my Customer's Scooter before ..
==
this motor is Okay for riding is rate 36 volts and speed about 30 mph
==
if you push voltage and it will burn the rewind inside the motor also ....
==
Alway Limit to 32 Volts for safety Rate contine running on motor.....
==
Craig Uyeda
Deafscooter
deafscooter
Deafscooter,
My controller is not programable, so, 36 volts is out of the question. It will supply an easy 100 amps, it is the Alltrax NPX 4834. I thought about 36 volts and limiting the throttle voltage, just for the sake of doing it. The law says 20 mph max in Texas, no reason around here to go any faster. Looked at the brushes in this motor, not any larger than the brushes in 6 amp 110 volt drills. If I was to go up in voltage, the brushes would have to be changed, the wiring is very beefy, I'd say the weakness is in the brushes for voltage increases, they seem to hold up, If the springs were stronger there is plenty of brush, about time for me to add new brushes, local alternator shop may have better springs, I will ask him when I order brushes. Not the best brushholders I've ever seen either.
chuck
[b]AGM BATTERIES[/b]
echuckj5,
I just think the chart is off. Lets forget the chart and go back to basics:
Heat is proportional to I^2. If you want less heat you need to reduce the current, and decreasing the gear ratio is NOT the way to do this because it will result in the motor needing to put out more torque to deliver a given amount of power, and power output is what is required to overcome friction and inertia for maintaining speed and accelerating.
If you want to reduce heating, than the best way to do that is lower the current requirements. If you want the same power output but don't want the same current than you have to raise the voltage. But because voltage is directly related to speed, and current to torque, to decrease the torque requirements for the same power output you have to raise the speed requirements. To do this you need to raise the gear ratio.
I suggest raising the voltage and increasing the gearing. Deafscooter said 32v is ok, so I'd add a 6v in series with your pack, and raise the gearing (or increase the gear ratio) so the top speed is the same.
P.S. I know there are lots of other factors that determine efficiency, but resistance dwarfs them all in an EV using a PM motor. A rule of thumb is the higher the gear ratio the better as long as you can maintain the speed you want.
---
Avatar taken from http://www.electricmotorbike.org/
My KZ750 Project: here
[url=/forum-topic/motorcycles-and-large-scooters/587-my-kz750-electric-motorcycle-project]KZ750 Motorcycle Conversion[/url]
[url=/forum-topic/motorcycles-and-large-scooters/588-fixing-my-chinese-scooter]900 watt scooter[/url]
Pic from http://www.electri
Yea Andrew,
My feeling exactly about switching to the 9.1 ratio from my current 10.4 ratio.
But, there are some strong merits to try the switch. It is finding the rpm where the design torque of the motor is strongest at 25 mph. A lot is happening in an electric motor, specifically in a series wound motor. I learned enough in Physics 25 years ago to pass my tests in the electric areas. I just was'nt interested in electronics and electricity at that time. I have reviewed the math behind the physics on electric motors, it is actually some of the most complex math out there. It would take me 2 or 3 months to relearn and apply that math. But basically, the motor is mathematically designed for a specific rpm at a given voltage. Going outside of those rpm parameters does introduce additional resistance, in my case it is showing up as the motor being to inefficient, iron core losses, hystersis, back emf, eddy currents ( more than I care to compute) all enter into the equation, more so on the high rpm range on the scott motor. The scott motor is designed as a torque motor. Its sole purpose originally is for 24 volt floor scrubbers.
According to the Bidwell Cheetah Manual, I should be getting about 16 miles in stop and go driving, hard driving, I get 12 miles at 25 mph. Best range according to his manual is about 25 miles, I get about 19 miles at 20 mph easy on the throttle driving. The Bidwell manual recomends an 8.9 to 1 ratio for the Cheetah. Ken at KTA services (where I bought my motor) recommends a 9.1 to 1 ratio to get the best efficiency from the scott motor in electrothon racing. MB-1E (AirBorne) made the switch, He seems quite satisfied using a slightly smaller scott motor.
I'm as stubborn as usastacy, I got it in my head that the reduction should have been in the 11 or 12 to one range. I have stuck to that for too long, almost 3000 miles, I have had that 16 tooth sprocket just laying there.
Changing to a 9.1 ratio requires me to replace my jackshaft 14 tooth sprocket to a 16 tooth sprocket, about 10 minutes of time. Since I have the sprocket, I'll make the change. See what happens
chuck
[b]AGM BATTERIES[/b]
Andrew and Chuck,
the chart isn't off, but you might want to look at the red line (current) in the diagram as well. It takes some studying of it to understand that most of your driving will be at the very left part of the diagram. Left of the black vertical line. So at 3200 rpm current is much lower than 41 A, and total losses (heat) much less than you calculated.
Changing the gear ratio will move your load point slightly to the right in the diagram, but not all the way down to 3000 rpm, since the speed will increase as well. Unless you lower the voltage, but that will require the complete diagram to be redrawn.
Changed the ratio to 9.1 from 10.4.
Results.
Range the same.
Speed has increased 3.5 mph
From a seat of the pants, acceleration less at 0 to 10 mph, pulls harder at 10 to 28 mph. Have never topped 30 mph in one year down the steepest grades, maximum speed ever recorded is 28.5, now 32.5 mph, cruising speed of 25.5 mph at the 10.4 ratio has increased to 29 mph at the 9.1 ratio.
Voltage drops during acceleration, cruising and up grades the same. Speed up grades was about 22.5 mph, now about 25 mph.
Motor temperature. Reduced, why, probably due to outside air temperatures aroung 85 F the last few days since I made the switch. With extremely hard driving, I do not have to remove my hand from the motor. At 10.4 to 1 and above 90 degree temps, the motor was untouchable.
Chain noise, reduced dramatically. The drive was always silent until I put the 14 tooth drive sprocket on it. That 14 tooth sprocket must have had some natural resonance to it. With a 15 tooth sprocket, original sprocket on the Cheetah about 6 or 7 months ago, I had no chain noise.
chuck
[b]AGM BATTERIES[/b]
Hi, On "Bike to the Future" we use a cheap Unite 1200 watt PM motor at 48 volts. The controller can do 40 amps and peaks around 100. With even 8:1 gearing, on hills, the motor still got angry hot. We added a brushless fan that only draws less than a third of an amp. No more problems! This could be a good thing to try on your Scott motor... Also, make sure your brakes are not constantly rubbing.
Jeff and Eddie K. Burbank, CA "Bike to the Future" and "Deep Cycle"
echuckj5, its good to hear that the mod worked well for you so far. Nothing beats trial and error. If your mod gives you results then there isn't any amount of calculations on paper that can dispute that. I hope the motor temperature doesn't go too high when the weather warms up. In the motorcycle discussion list there are more and more people with etek failures because they are running them way too hot. You may be stressing that 1 hp scott motor to the limit.
[url=/forum-topic/motorcycles-and-large-scooters/587-my-kz750-electric-motorcycle-project]KZ750 Motorcycle Conversion[/url]
[url=/forum-topic/motorcycles-and-large-scooters/588-fixing-my-chinese-scooter]900 watt scooter[/url]
Pic from http://www.electri
Andrew,
Awhile back, Fechtor said, "If spit does'nt sizzle on the motor, you are probably alright as far as motor temp."
My motor has been hot, I am guessing 125 to 130 degrees. I could not keep my hand on it but for just a few seconds. Not near hot enough to cause spit to sizzle. Now the temperatures are in the low 80's as compared to the low 90's, after the change of gear ratio's I can place my hand on the motor comfortably.
1 hp calculates out to 27 mph. So I should be in the proper load range. Per the chart above, over revving a series wound motor causes efficiencies to drop. The speed ratio and given load per the chart is what I am trying to match. By matching the motor to the load. Matching the rpm of the motor to the load. It would seem to me that it is more effiecent overall to run the motor at the design rpm per a given load.
When I get around to it, I'll put an amp meter on it. I need to find a temperature sensor to find out what my actual motor temps are. Keep a log. Be a little more scientific.
Results so far, driving just as hard as before the gearing change. Air temperatures have dropped 10 degrees.
Motor temperature much cooler.
Speed has increased almost directly proportional to the gearing change.
Range is the same.
Voltage drop at 25 mph is less, about .8 volts, from the previous of about 1.2 volts.
chuck
[b]AGM BATTERIES[/b]
Need to start keeping a log. Be a little bit more scientific.
Has the gearing change helped, oh yeah.
Found the flattest road in Texas, not as easy as you think around here. Going due south, 5mph headwind "estimated". Very slight downhill. 30.5 mph, 1.2 miles. Turn around, now it is a slight tailwind, but slight uphill, 29.5 mph.
The extra speed is nice, keeps me up with traffic. Does'nt do a whole lot for range. Motor temps, are much better when I drive at the old 25.5 mph. Range, still have not been able to find the time to verify the difference by actually driving the distance. Going by just voltage, let me find my figures, they are here somewhere,
10.4 to 1 ratio, hard driving, top speed 25.5 mph, 5.37 miles. over 5 days, Northbound trip, mornings only, ending voltage 12.22 volts
9.1 to 1 ratio, hard driving, limiting my top speed to 25.5 mph, same trip profile, ending voltage over 5 days, 12.37 volts
12.22 volts is just very slight less than 49% of my battery used.
12.37 volts is probably just about 38% of my battery pack used.
Why go 25.5 mph? That is the old top speed using 10.4 to 1 gearing, on average. With my new gearing 25.5 mph is supposed to be, according to the above chart, the most effiecent rpm of the motor. Has it made a difference. Seems to have made a signicant difference. More torque, except at startup, but, my controller limits the starting current and is not programmable. Drivetrain noise reduced, a lot.
Thrill, big difference between 25.5 and 29 mph. Feel like you are getting somewhere.
I am not trying to go faster though, trying to go farther, next chance I get, I will do a true range test at max speed of 20mph
Range at 30 mph, forget it, not worth mentioning
chuck
[b]AGM BATTERIES[/b]
c
[b]AGM BATTERIES[/b]
Chuck,
this is good stuff. I would like to contribute with some clarifications. You write "With my new gearing 25.5 mph is supposed to be, according to the above chart, the most effiecent rpm of the motor." Actually, the chart doesn't necessarily say that. What you have done is changed the gearing, so that for a specific speed (25.5 mph), the motor will run at lower rpm. What more has changed? The output power should be about the same, so at lower rpms the torque must be higher. The voltage is lower, and the current is higher.
The chart is drawn for a specific voltage (24 V), but for other voltages, the curves will be different. The maximum efficiency will be reached at a different rpm. With some guessing, I would say the voltage at 25.5 mph before the gear change (full throttle) was perhaps 23 V, due to the voltage drop of the controller. After the gear change the motor voltage should be around 19.5 V.
Your measurements indicate that for the same distance, energy consumption is reduced to 38% of a full charge, from 49%, by changing the gearing. If that is true, motor current at the higher gearing (lower rpm) is 23/19.5 * 38/49 = 91 % of the current at the lower gearing? (Assuming the losses in the controller are the same, which is a good approximation mostly. And not counting the peukert effect.)
So when changing the gearing with a factor 1.14, you are running the motor at higher torque, but at lower voltage AND current. And efficiency has gone up 29%? (Example: from 66% to 85%) I find this hard to believe - but you don't have to convince me. Before believing it yourself though, you might want to make some more measurements.
And this discussion about efficiency doesn't exclude the rewarding feeling of higher top speed. I would probably have done the same mod.
Regards,
Rolf
rgx,
Data collection, virtually nonexistant. Real World Performance, range never at my expectations. I'll get around to better data collection. I never tried measuring motor current, that would be a lot easier to calculate.
For about a year, I ride to work, 5.7 miles. Battery pack about 1/2 empty. 12.2 volts. Conditions, Dallas is a windy city. Normal winds are 15 mph with gusts. I made the gear change and for a week, temps were about 75 F in the mornings, no wind, very pleasant. Taking the effect of the wind away, and temp. certainly skewed the results.
The State of charge chart, provided with the batteries, for the odyssey batteries is linear. It says my batteries are 1/2 depleted at 12.2 volts. I go farther on the first 1/2 of my pack, using the state of charge chart, than I do on the second 1/2 of the battery pack.
I am trying to go farther, not faster. The results that matter to me most.
Wide open throttle, 25.5 mph, 10.4 gear ratio, 5.7 miles, battery voltage 12.2
4/5 throttle, 25.5 mph, 9.1 gear ratio, 7 miles, battery voltage 12.2.
That is about a 20% increase in distance. 3 trials with more or less similar conditions. Temperatures, about 95 degrees, near normal winds.
I only have one week of results, I no longer work 5.7 miles from home, new work is 16 miles, farther than the 864 watt pack can take me. Not a bike friendly route, so, testing is over.
Using these calculations,, 10.4 reduction and 25.5 mph, motor rpm is 3273. At 25.5 mph, motor rpm is 2864. About 12.5% reduction in motor speed,
The chart provided by KTA Services, tells me at 3273 rpm, motor is about 60% efficient, at 2864 rpm, the motor is 82% efficient. I need about 750 watts to go 25.5 mph. By the chart, at the higher rpm, total watts used should be about 1250. By the chart, at the lower rpm, total watts used should be about 914 watts, which is about a 27% decrease.
So, Real World Results. Motor is not near as hot. 2 to 3 mile increase in distance, at 25 mph. Range, really guessing, 13 to 14 miles. Range was about 11 miles at 25 mph. Drive train noise, reduced a lot, probably 75% in noise.
I'm happy
chuck
[b]AGM BATTERIES[/b]
There seems to be some confusion on torque, it can be measured a lot of ways.
If the chart is correct, it looks like a hair more than 1 hp. From the chart, oh about 2.3 ftlbs of torque. Get my units right, need mph of 25.5 into ft/s,, 25.5m/hr * 1hr/3600sec * 5280ft/1mile = 37.4feet/sec
power = work/time
1 hp = 550ftlbs/s
Torque=force*distance
velocity = distance/time
work = force * distance
Velocity = 37.4 feet/sec
torque, from chart, =2.3 ftlbs
radius of the wheel=1.135ft
lever of the wheel is = 1 / 1.135 feet = .88 feet
power = 1 hp = work/time = force*distance/time,, looking for force so I can get torque, rearrange, power*time/distance=force
Force = 14.7 ftlbs
Force=550/37.4 = 14.7ftlbs, motor only putting out 2.3 ftlbs of torque, need to get some more leverage, how, gear it down, I geared it to 9.1 to 1, this can be done simpler, using radians, I'll stick to the simplest way, the torque at the wheel on my bike.
torque at the wheel = torque of motor * reduction * lever of the wheel =
2.3lbs * 9.1 * .88ft = 18.4 ftlbs. I only need 14.7 ft lbs to cruise at 25.5 mph, by the chart, I am still not loading the motor down.
Now, lets do a check, because torque and hp are directly related.
1hp = torque * rpm/5252 torque from chart,2.3 * 3000rpm/5252 = 1.31 hp, charts wrong.
Ken at KTA services, sent me a chart that is Copyright protected, so I cannot post it here, Ken says the scott motor is rated at 1.2 hp, about 2ft lbs of torque at 3050 rpm. Check Kens numbers, 2*3050/5252 = 1.16 hp, Kens' chart is closer. A lot closer
Charts are charts, I can backwards engineer most charts, get the information I need. Looks like Scott motors need to redraw their chart. Why I am using the chart from KTA services, Ken supply's kits for electrathon racing, these numbers, to win, need to be correct.
chuck
Now, where did I get that It takes 1 hp to go 27 mph, krueztter's bicycle calculator,
Using several different coefficients of drag, from sail making to cliff diving, I found that 1 hp was a slightly high estimate, figure the wind and other factors, probably pretty close.
Now, If I get Airborne to launch off a cliff, freefall on his bike, pull a chute just before he lands, I can calculate a very good coefficient of drag, from the difference between how fast he falls, versus what the gravity calculation says he should fall.
Just have to make sure he packs his own chute.
[b]AGM BATTERIES[/b]
Watt and distance calculations.
I said my motor was getting hot, I talked to Dave, MB-1-E, I kept wanting to know how hot His motor was getting, I was gearing lower and lower, Dave was gearing higher and higher. Dave kept telling me that He was not having the heat problems I was.
Old reduction ratio was 10.4 to 1. Motor rpm was 3273 at 25.5 mph
New reduction ratio is 9.1 to 1. Motor rpm is 2864 at 25.5 mph
Total watts = (VI + I^2R) VI is the power,, I^2R is the loss
AT 3273 rpm the motor is 65% efficient, from the chart above. The chart from KTA services says 60%. Because I am interested, this is my motor, I am going to use Ken's chart, which I showed in my last post as being correct.
Power at the wheel is 750 watts at 3273 rpm.
The total watts going to the motor is 750 watts/.60eff = 1250 watts
The I^2R losses are difference between 1250 watts and the 750 watts I am using. That difference is heat. 500 watts of Heat. Wonder why my motor is getting hot.
At 2864 rpm, still using 750 watts to move at 25.5 mph.
Using Kens' chart again, effiency is 82%
Total watts going to the motor is 750 watts/.82eff = 914 watts
The I^2R losses are 914 watts - 750 watts. Hmm, thats 164 watts.
I use the odyssey batteries, their chart says at the 1/2 hour rate, use .66 to calculate the available power.
Pack wattage of 864 watts*.66 = usable watts of 570
Range, using the old ratio. (570/1250)*25mph = 11.4 miles
Range, using the new ratio. (570/914)*25mph = 15.6 miles
Now, I have stops and starts, hills to climb. 15.6 miles would be a steady rate.
I have a lot more torque. The watts that were being diverted to heat, are now available, kind of a reserve amp supply.
Results are still the same, motors cooler, I am using less battery per ride.
Batteries are getting old, one pair is a year old, 2nd pair is 7 months old. Slightly over 3000 miles on the motor. How far can I go, try to answer that this weekend.
chuck
[b]AGM BATTERIES[/b]
echuckj5, this and what I'm hearing from PJD about his scooters is changing my perspective somewhat. Interesting stuff! But can you get some real measurements to help confirm it? My stubborn self is still not convinced =P.
I guess I need to crack open some text books and get studying motors. I remember a few of the losses such as hysteresis, core loses, magnetic loses or something like that. The I^2R should just be heat loss due to current flow, which are resistive losses. Current should always go up in a DC motor as you slow it down to get more torque. As the current goes up, the resistive losses will always rise.
So my guess is that there are more resistive losses, but the other losses are much less. Some of them can apparently be quite significant. For example, you have to torque an etek down enough to draw 20 amps for it to be reasonably efficient from the graphs.
And another factor is brush timing. Running a motor at high speed needs the timing to be properly advanced both to reduce arcing and for optimal switching of the coils.
[url=/forum-topic/motorcycles-and-large-scooters/587-my-kz750-electric-motorcycle-project]KZ750 Motorcycle Conversion[/url]
[url=/forum-topic/motorcycles-and-large-scooters/588-fixing-my-chinese-scooter]900 watt scooter[/url]
Pic from http://www.electri
Now, how many amps am I using? Feel free to jump in, I don't know the resistance of this motor, AND, I am estimating the voltage. There is a better way to solve three variables, been to long since I took math. I played with it, should be pretty close.
Total watts = VI + I^2R
I don't know what my motor resistance is. I don't know my current either.
Watts I^2R = 164 watts
Watts Power = 750 watts
Watts Total = 914 watts
Voltage est. = 24 volts
Power = 750 watts = 24v*I,, re-arrange to find I, 750/24=31.25 amps
Wasted watts = 164 watts = (31.25)^2* R,, re-arrange to find R, 164/31.25^2 = .168 ohms
Check the math,, Total watts 914 = 24v*31.25 + (31.25)^2(.168)
= 750 + 164
= 914 watts
Went on a ride today. Was going to see how far I could go. Tried to keep the speed up to 25 mph. Had to go thru some 20 mph school zones, which dropped my speed. Very good results. Starting voltage was 12.97, thought this was strange, did not check the voltage of the front pack. Normally, each pack is about 13.05. Only had one voltmeter, hooked up to the rear battery pack.
Starting voltage: 12.97 volts
Ave speed: 18 mph
Top speed: 28.5 mph
At mile 7.49,, the rear pack was at voltage 12.2 after stopping and letting the voltage stabilize for a couple minutes, very good results, almost 2 miles farther than before.
At mile 8.29, rear pack voltage was 12.1 ,,. Was at my parents house, visited with Dad, planted some more in the garden, stayed about an hour, pack voltage, rear, had risen to 12.25 volts.
At mile 10, rear pack voltage, just plummeted, little power, hmm, something wrong. Right rear battery is warm, all three others are normal. Limp home at about 15 mph.
At mile 11.84, I am home. Rear pack voltage, after a few minutes of stabilizing, is 11.2 volts. Front battery pack is 11.78 volts. That one battery is warmer, put a fan on it, let it cool, then charged it up. Both packs took the same amount of time to charge, pack with bad battery took a couple minutes, maybe five, longer to charge. The bad battery was slightly warm, other three normal.
Well, I got some batteries to load check, Battery in my car is needing replacing from disuse, probably put a pair of these in the car, buy some new batteries. Use the remaining good battery to run my lights at 12 volts.
chuck
[b]AGM BATTERIES[/b]
hmm, the battery that was warm is buddy paired with another one right? Why was it getting warmer than the others? Maybe it has a cell that went out and is getting reversed?
I'd bet one of these batteries can start your car. Of course two doesn't hurt. I'm very interested in that bad Hawker. I wonder if I could trade you something for it. I want to see if I can use my mad scientist techniques to bring it back.
[url=/forum-topic/motorcycles-and-large-scooters/587-my-kz750-electric-motorcycle-project]KZ750 Motorcycle Conversion[/url]
[url=/forum-topic/motorcycles-and-large-scooters/588-fixing-my-chinese-scooter]900 watt scooter[/url]
Pic from http://www.electri
Andrew,
Might be warm because it is doing all the work and the other battery it is buddy paired with is bad.
Man oh Man, I been busy, let me play with it a little. Bought it at Batteries plus just down the road 7 months ago. These, also, are the 2 newer batteries.
I never conditioned these by cycling them. Pretty much 90% of their use was a trip 5.7 miles, on the charger, 5.7 miles home, then on the charger, 5 days a week, an occasional trip to my Parents, 3.7 miles away, or the grocery store. Probably have 1500 miles on these.
If Battery Plus does'nt warranty it, I'll send it with your charger, I have'nt forgot, just got to get some free time to get it sent, Will I need a haz mat label on it, I think I have the original box.
Also, I don't charge people for what I consider ""gaarbbagge", don't worry about it.
chuck
[b]AGM BATTERIES[/b]
Andrew,
Here's 2 electrical engineers discussing a motor, both have the same output, same rpm, one is 48 volts, one is 24 volts. Same I^2R losses
http://endless-sphere.com/forums/viewtopic.php?t=967
Now, when a 24 volt motor is overvolted to 36 volts, something different happens, yes, I calculated the I^2R losses, would save another, about 90 watts, on the I^2R, reducing my loss from 164-90, to about 74 watts, nice eh.
The truth is in the pudding, now everyone has to put blowers on the motor for cooling. Where is that heat coming from, I call it MBO. And, if I overvolt, I have to increase my gear reduction another 50%. Now the equation is, for overvolting,
Total Watts = VI + I^2R + (MBO).
(MBO) is motor burning up. I understand why, could have calculated it 25 years ago, Magnetic fields don't turn off and on instantly, they leave, is it gauss or henry's, behind, they are still diminishing, now the new field is interfered with by the old magnetic field. A tubulence effect, and, as the the power out increases, I have to increase the amps to stabilize the newly generated field. There are also the effects of left over magnetism, for lack of a better word, generating other offsetting magnetic fields. Some motors are wound differently, they have a very flat effiecency curve, the scott motor does not have that type of structure.
chuck
[b]AGM BATTERIES[/b]
Hi Chuck,
I don't want to hi-jack your thread so I'll start one of my own about my 3/4 hp Scott but this one sure has some good information. Most of this is way over my head but I've been trying to follow along none the less.
As Chuck mentioned, I have a 3/4 hp (560W) 24V Scott.
With 36Ah @ 24V I think I have nearly the same battery capacity as Chuck has.
Even though I'm extremely pleased with what I'm getting out of my system, I'm still interested in exploring the pros and cons of going over voltage and/ or going with different gear ratios.
As for this cliff jumping business and pulling the chute at the last minute, I really don't think that there is any way to get good quantitative data from such an experiment so I think I'll decline to offer my services in this regard.
Oh, and as far as packing my own chute ... no thanks, I may be crazy but I'm no fool ;)
Dave B
MB-1-E
<a href="http://visforvoltage.org/book-page/996-mountain-bike-conversion-24v-3-4h... - Bridgestone MB-1 Mountain Bike</a>
Total watts = VI + I^2R
A few more comments, I said jump in when I was finding the three unknown variables.
This equation is a 2nd degree polynomial, handled in high school algebra, by factoring.
Plotted and solved very easily, using chapter one of calculus, take the 1st derivative to find the slope at any point of the curve that the above equation plots out. I could sit down for a couple of evenings, relearn some easy calc, plug in all kinds of scenarios, and get very accurate results. Lots of handheld calculaters can handle this. If you know an engineer, sit down with them, they can solve this quick.
To solve this problem, I used the conservation of energy, all inputs must be accounted for. I solved the problem from the outside. Some processes are so very complex that actual measurements of the process are not attainable, so we look at it from the outside. It is not really important, on a case by case basis, to find where the I^2R losses are coming from.
These losses can be calculated. If I was designing a motor, these would be my engineering costs. I would tell an electrical engineer my requirements, the engineer would have to overcome all the design problems, and, get the effiency, "conservation of energy" to an acceptable level. There is no 100% efficient conversion of electrical energy into mechanical energy. The motors that are peaking at 90 and 95% efficiency, are doing that at a very pronounced efficiency, arched, curve. They are designed to be very efficient at a very narrow rpm range.
I want to look at the etek, the pmg, and the advanced dc motor curves. I have to choose a motorcyle and a motor. If I buy a motorcycle first, I have to accept a motor that fits. If I buy a motor 1st, then I have to accept a motorcycle that fits. There are trade offs.
I think, without looking at the curves, just a few that I have seen online, that the efficiency curve of the advanced motor is the flattest, that flatness comes with the cost of a lower peak efficiency and weight. And size. Losing peak efficiency is good, because I travel all different speeds, encounter hills, wind. Lose peak efficiency, gain overall efficiency.
chuck
[b]AGM BATTERIES[/b]
[Note: This post was edited by Revolted (the mod account for andrew) On Oct. 6 2007 at 15:45 GMT]
Its important to consider voltage change when considering overalls though. The curve at the top is for one voltage. Your controller changes the voltage to the motor. I like to think of it as if one accelerate slowly during starts than they are riding the efficiency curve so to speak. Your 25.5 mph is not top speed so the controller has to be limiting the voltage. From the curves at various voltages for say the etek one can see that the peak and overall efficiency is lower at lower voltages.
I^2R losses are exclusively the electrical resistive losses. This is because it is, fundamentally, the voltage drop times the current. And the voltage drop is what resistance causes. Looking at V = IR lets say a motor is drawing 100 amps at 30 volts. Lets say the terminal resistance is .1 ohms.
The voltage drop in the circuit (or the potential loss due to resistance) = (100 amps) * (.1 ohms) = 10 volts.
Since there is 30v and 100 amps going into the system, every volt at 100 amps is going to represent 100 watts in power. So the potential drop of 10v * 100 amps = 1000 watts in resistive losses which shows up as 1000 watts in heat. You can condense this into I^2R, but what one doesn't see in I^2R is that they are actually calculating the potential drop due to resistance then multiplying by the current because the math is condensed.
If there were no other losses then the motor would be putting out (30v * 100 amps) - (1000 watts in heat) = 2000 watts in kinetic energy. However there are other losses which will also show up as heat, but are not resistive losses. Due to conservation of energy, every loss will either show up as heat, or something, such as air moving out of the motor.
One can see these "other losses" in the no-load current draw of a motor. The etek, for example, draws 7 amps at no load. At 48v thats 336 watts. One can now see clearly that they have to load an etek down to raise the efficiency. If it is loaded down to 8 amps than:
The resistive losses are: 8^2 * .033 (terminal resistance) = 2.112 watts
The other losses are 7 (no load current) * 48 = 336 watts - 7^2 (resistive losses at no load) * .033 = 334.38 watts.
The power output is: [power in] - [(no-load losses) + (resistive losses)] = [power out] I'm sure thats oversimplified as I'll bet some of the infamous "other losses" become greater with more current due to higher magnetic fields. In any case thats: 384 - [334.38 + 2.112] = 47.5 watts.
The efficiency is: [power out] / [power in] = .124 or 12.4% efficient.
I'm guessing something similar is happening in the case of the Scott motor. This is where the no-load losses are high. Lets say, however, that the no-load current is about the same at all voltages (though it drops rapidly at very low voltages). So if the voltage is halved but the same amount of power is put in in than the no-load losses will only be half as much.
24 * 7 ah (no load current) - 7^2R (resistive losses at no-load) = 166.38 watts no-load losses (non-resistive).
So to put the same amount of power in the current needs to be doubled, or go to 16 amps input. This means more resistive losses. You areI'm actually raising the resistive losses or I^2R losses, but lowering the other losses by a lot, and the result is increased efficiency.
16^2 * .033 = 8.448 watts resistive losses, quite a bit more than 2.112 watts at 48v, but still almost insignificant.
The new power output is: 384 - [166.38 + 8.448] = 209 watts. Quite amazing huh!
The new efficiency is: [209] / [384] = .544 or 54.4% efficient. So I've just quadrupled the I^2R losses and increased the efficiency by more than 4 times by halving the voltage and doubling the current? Yes because I've reduced the no-load losses or the infamous "other losses" by lowering the voltage. Even though I've increased the resistive losses, they are still relatively insignificant.
Something like this is what I think is happening in the case of the Scott motor. Though this is much more of an extreme example to illustrate the point. I'm sure resistive losses in that case are significant, they just happen to be not as significant as no-load losses (which include all the other infamous "other losses"). In this way one can increase the current and increase the resistive I^2R losses but raise the efficiency because they are reducing the no-load losses by running the motor at a slower speed.
[url=/forum-topic/motorcycles-and-large-scooters/587-my-kz750-electric-motorcycle-project]KZ750 Motorcycle Conversion[/url]
[url=/forum-topic/motorcycles-and-large-scooters/588-fixing-my-chinese-scooter]900 watt scooter[/url]
Pic from http://www.electri
Andrew,
I think you lost me.
So, use the no load scenario, and apply it using the data I have supplied, use the scott motor information. Well, unfortunately, not enough information.
Qoute
"Lets say, however you get smart"
That is your qoute Andrew, from the above, is that directed at me? If it is'nt directed at me, please edit your post, and take all the "you's" out. Then I will edit this post, I am watching my blood pressure, ,,,, seriously Andrew
qoute
"I^2R losses are exclusively the electrical resistive losses. This is because it is, fundamentally, the voltage drop times the current. And the voltage drop is what resistance causes. Looking at V = IR lets say a motor is drawing 100 amps at 30 volts. Lets say the terminal resistance is .1 ohms"
Andrew, the above, the voltage drop at the motor, the motor being the resistor, that times the current is the (power out). The resistive losses now are from a different system, the battery current, the battery voltage, the controller losses, and the line losses, the motor as a resistor. The controller as a resister. The cables as a resistor. Now the resistive losses are your I2R losses, and, all the energy can be calculated. You are absolutely correct. What is happening inside the motor can 100% be disregarded, solving for inefficiency, by doing it this way. The motor now is a variable resistor in the circuit that "you" are trying to calculate.
I, "chuck" find that this is a very difficult way to find the efficiency of a motor, in Real World Scenarios, it can be done, data collection will be an absolute nightmare. To do it accurately, I would say that all this information would have to be collected at a maximum of 5 second intervals, probably for good results on 1 second intervals. My trip profile is about a half an hour. You would need to get from 360 to 1800 sets of data. Place your I^2R data on the y axis. Time will be the x axis. Plot the data, find the area under the data curve, subtract that from the estimated PE of the battery, and now, you should come up with an answer similar to mine.
Andrew, Qoute
Since there is 30v and 100 amps going into the system, every volt at 100 amps is going to represent 100 watts in power. So the potential drop of 10v * 100 amps = 1000 watts in resistive losses which shows up as 1000 watts in heat. You can condense this into I^2R, """"but what you don't see""" in I^2R is that you are actually calculating the potential drop due to resistance then multiplying by the current because the math is condensed.
What don't I see Andrew?
I understand, basically, where you are going with this, lets use my data from above, and apply it.
My battery voltage never drops 10 volts, under hard acceleration it drops 2 volts.
My current changes from 0 amps to probably 100 amps.
My motor, will have resistance equal to the voltage drop at the motor * current.
I guess, collect the data on 1 sec intervals?
Now, what I am trying to solve is the way to get the maximum energy from my battery by running the motor at the rpm's that allow the motor to use its its inputs to a maximum.
I have not tried to solve the original problem, limited range and a hot motor, using Andrews' method, I will have to think about this and see how it could be done.
I do understand, Andrews perspective, doing it Andrews way does eliminate the I^2R losses that are internal to the motor, in the calculations. How to supply the information that I need, using Andrews method, hmm, let me think about it for a couple days, off the top of my head, seems like a more difficult way to approach the problem, looking at the input side, not the output side. I looked at the problem from the mechanical outputs, not the electrical inputs. Now, how to solve for the I^2R losses inside the motor doing this?
chuck
[b]AGM BATTERIES[/b]
Chuck, I took most or all of the you's out. Sorry I didn't realize how many times I addressed you, and it was quite a job editing. No offense intended!
Removed this.
I know this information is very dense, and I don't mean to be overbearing. This is just my view point, take it for what its worth.
It doesn't take any elaborate measurement method to calculate the I^2R losses. The terminal resistance (or the resistance of the motor at the motor terminals) does not change. It is constant. Once you know the resistance you can calculate the I^2R losses with any given motor current. The I^2R losses are independent of motor speed or anything other than the current and the motor resistance. To measure it, a constant voltage can be applied across the motor terminals and the motor can be stalled or held from moving. If the voltage is measured at the motor terminals, and the current of the circuit is known than the resistance can by calculated:
V = IR, R = V/I
If the motor moves at all than it generates a so called "back EMF" or just a potential that will lower the amount of current that will flow. This is why, say x motor has constant resistance, the maximum current it can draw drops as it speeds up. The maximum current that any motor can draw is:
[applied voltage] - [back emf] / [motor resistance]
This means if the motor is stalled than the amount of current that will flow is a function of the motor resistance and the voltage.
So to measure the motor resistance the motor needs to be stalled. It shouldn't matter how much voltage is applied. To get an accurate resistance, allow the motor to rotate very slowly while holding the shaft and watch the voltage (if it is a CC power source) or current (if it is a CV power source) or either (if it is a battery) and at either the lowest voltage value or the highest current value write the current and voltage down.
I calculated the etek resistance of .033 ohms from the motor graphs, but I think I got something close with a resistance check. Only, the etek brushes tilt slightly in their holders if the motor is rotated counter to its normal direction of rotation so I think this messed up the results, and at the time I didn't know this was happening. To calculate the etek resistance accurately the motor needs to be first broken in, and it needs to be rotated only in the direction of normal rotation between measurements.
[url=/forum-topic/motorcycles-and-large-scooters/587-my-kz750-electric-motorcycle-project]KZ750 Motorcycle Conversion[/url]
[url=/forum-topic/motorcycles-and-large-scooters/588-fixing-my-chinese-scooter]900 watt scooter[/url]
Pic from http://www.electri
Andrew, now I can't edit my post,
Do me a favor, my bike is down, batteries all over the place, so I can't do it.
Attach a volt meter to your motor, and ride motorcycle, watch the voltage drop. at the motor, then post those numbers. Try to get a number at 10 mph, 20, 30, 40.
What is being measured in the last post is correct, that is the resistance of the total length of wire in the motor. That resistance will change with heat. Measure it cold, Measure it hot. That will not account for all the I2R losses, in the motor. Just the winding losses.
What you are saying, to me, I think, is that that should account for all of the I2R losses. In the motor.
chuck
[b]AGM BATTERIES[/b]
hmm. I thought it would account for all the I^2R losses but maybe I'm wrong. I thought I^2R losses are exclusively winding losses due to resistance. I've not thoroughly studied motors or have the technical background to say for sure though. What other losses could be I^2R losses? I don't think I see how there could be any.
[url=/forum-topic/motorcycles-and-large-scooters/587-my-kz750-electric-motorcycle-project]KZ750 Motorcycle Conversion[/url]
[url=/forum-topic/motorcycles-and-large-scooters/588-fixing-my-chinese-scooter]900 watt scooter[/url]
Pic from http://www.electri
I have several engineering manuals, they are available, most everything in them I have studied, except the electronics, as a physics major. So, I am opening the book to direct current machinery.
Nomenclature and units of measurement.
E volts: is the emf generated in armature
V volts: terminal potential or voltage
I amperes: line current
I1: shunt field current, we are using magnets so, don't know how to calculate
If amperes: series field current
Is amperes: armature resistance gbetween the brushes
Rf ohms: Series field resistance
Rs ohms: Number of poles
Nf: series field turns per pole, we are using magnets, so I don't know how to calculate
Ns: number of armature paths between terminals
m : number or armature conductors
Z: magnetic flux per pole
maxwells: armature speed
n: revolutions per minute
T: pound feet.
Now there are exactly 14 equations in this book, which is very condensed, just for the series wound motor, need all of these inputs to calculate the total losses.
Qoute, from the engineer manual
"To detemine the rotation losses corresponding to a definite load the motor at no load, must be run at the same speed and with the same emf as when running at the definite load."
There are about 10 more hints, in this manual, so that no mistakes are made, this manual covers many other types of motors, these are for series wound.
get your slide rule out, I took the math, it is extremly complex. It would take me months to relearn, all trig functions, all calculus,
But, after you take the load calculation from the pd on the motor, put the motorcycle on a kick stand, take the same readings, at the same motor rpms, should see efficiencys really go up as you increase velocity.
chuck
[b]AGM BATTERIES[/b]